Mean Reversion: Gravitational Super Force or Dangerous Delusion?
In my last post on the danger of using single market metrics to time markets, I made the case that though the Shiller CAPE was high, relative to history, it was not a sufficient condition to conclude that US equities were over valued. In the comments that followed, many disagreed. While some took issue with measurement questions, noting that I should have looked at ten-year correlations, not five and one-year numbers, others argued that this metric was never meant for market timing and that the real message was that the expected returns on stocks over the next decade are likely to be low. I was surprised at how few brought up what I think is the central question, which is the assumption that the CAPE or any other market metric will move back to historic norms. This unstated belief that things revert back to the way they used to be is both deeply set, and at the heart of much of value investing, especially of the contrarian stripe. Thus, when you buy low PE stocks and or sell a stock because it has a high PE, you are implicitly assuming that the PE ratios for both will converge on an industry or market average. I am just as prone to this practice as anyone else, when I do intrinsic valuation, when I assume that operating margins and costs of capital for companies tend to converge on industry norms. That said, I continue to worry about how many of my valuation mistakes occur because I don’t question my assumptions about mean reversion enough. So, you should view this post as an attempt to be honest with myself, though I will use CAPE data as an illustrative example of both the allure and the dangers of assuming mean reversion.
Mean Reversion: Basis and Push Back
The notion of mean reversion is widely held and deeply adhered to not just in many disciplines but in every day life. In sports, whether it be baseball, basketball, football or soccer, we use mean reversion to explain why hot (and cold) streaks end. In investments, it is an even stronger force explaining why funds and investors that fly high come back to earth and why strategies that deliver above-average returns are unable to sustain that momentum.
In statistics, mean reversion is the term used to describe the phenomenon that if you get an extreme value (relative to the average) in a draw of a variable, the second draw from the same distribution is likely to be closer to the average. It was a British statistician, Francis Galton, who first made official note of this process when studying the height of children, noted that extreme characteristics on the part of parent (a really tall or short parent) were not passed on. Instead, he found that the heights reverted back to what he called a mediocre point, a value-laden word that he used to describe the average. In the process, he laid the foundations for linear regressions in statistics.
In markets and in investing, mean reversion has not only taken on a much bigger role but has arguably had a greater impact than in any other discipline. Thus, Jeremy Siegel's argument for why "stocks win in the long term" is based upon his observation that over a very long time period (more than 200 years), stocks have earned higher returns than other asset classes and that there is no 20-year time period in his history where stocks have not outperformed the competition. Before we embark on on examination of the big questions in mean reversion, let's start by laying out two different versions of mean reversion that co-exist in markets.
In time series mean reversion, you assume that the value of a variable reverts back to a historical average. This, in a sense, is what you are using when looking at the CAPE today at 27.27 (in August 2016) and argue that stocks are over priced because the average CAPE between 1871 and 2016 is closer to 16.
In cross sectional mean reversion, you assume that the value of a variable reverts back to a cross sectional average. This is the basis for concluding that an oil stock with a PE ratio of 30 is over priced, because the average PE across oil stocks is closer to 15.
At the risk of over generalization, much of market timing is built on time series mean reversion, whereas the bulk of stock selection is on the basis of cross sectional mean reversion. While both may draw their inspiration from the same intuition, they do make different underlying assumptions and may pose different dangers for investors.
The nature of markets, though, is that every point of view has a counter, and it should come as no surprise that just as there are a plethora of strategies built around mean reversion, there are almost as many built on the presumption that it will not happen, at least during a specified time horizon. Many momentum-based strategies, such as buying stocks with high relative strength (that have gone up the most over a recent time period) or have had the highest earnings growth in the last few years, are effectively strategies that are betting against mean reversion in the near term. While it is easy to be an absolutist on this issue, the irony is that not only can both sides be right, even though their beliefs seem fundamentally opposed, but worse, both sides can be and often are wrong.
Mean Reversion: The Questions
You can critique mean reversion at two levels. At the level at which it is usually done, it is more about measurement than about process, with arguments centered around both how to compute the mean and the timing and form of the reversion process. There is a fundamental and perhaps more significant critique of the very basis of mean reversion, which is based on structural changes in the process being analyzed.
The Measurement Critique
Let’s say that both you and I both believe in mean reversion. Will we respond to data in the same way and behave the same way? I don't think so and that is because there are layers of judgments that lie under the words “mean” and “reversion”, where we can disagree.
On the mean, the numbers that you arrive at can be different, depending upon the time period you look at (if it time series mean reversion) or the cross sectional sample (if it is a cross sectional mean reversion), and you can get very different values with the arithmetic average as opposed to the median. With cross sectional data, for instance, the oil company analysis may be altered depending on whether your sample is of all oil companies, just larger integrated oil companies or smaller, emerging market oil companies. For time series variations, consider the historical time series of CAPE and how different the "mean" looks depending on the time period used and how it was computed.

On the reversion part, there can be differences in judgment as well. First, even if we both agree that there is mean reversion, we can disagree on how quickly it will happen. That has profound consequences for investing, because there may be a time horizon threshold at which we may not be to devise an investment strategy to take advantage of the reversion. Second, we can disagree over how the metric in question will adjust. To illustrate, assume that the mean reversion metric is CAPE and that we both agree that the CAPE of 27 should drop to the historic norm of 16 over the next decade. This can be accomplished by a drop in stock prices (a market crash) or by a surge in earnings (if you can make an argument that earnings are depressed and are due for recovery). The implications for investing can be very different.
In summary, there is a lot more nuance to mean reversion than its strongest proponents let on. One reason that they try to make their case look stronger than it is may be because they are selling others on their investment thesis and hoping that if they can convince enough people to make it self fulfilling. The other, and perhaps more dangerous reason, is to convince themselves that they are right, as a precursor to action.
The Fundamental Critique
The process of mean reversion is built on the presumption that the underlying distribution (whether it be a time series or cross sectional) is stationary and that while there may be big swings from year to year (or from company to company), the numbers revert back to a norm. That is the elephant in the room, the really big assumption, that drives all mean reversion and it is its weakest link. If there are structural changes that alter the underlying distribution, there is no quicker way to ruin that trusting in mean reversion. The types of structural changes that can cause distribution to go awry range the spectrum, and the following is a list, albeit not comprehensive, of why these changes in the context of mean reversion over time.
The first is aging, with the argument easiest to make with individual companies and more difficult with entire markets. As companies move through the life cycle, you will generally see the numbers for the company reflect that aging, rather moving to historic norms. That is especially true for growth rates, with growth rates decreasing as a company scales up and becomes more mature, but it is also true of both other operating numbers (margins, costs of capital) as well as pricing metrics (price earnings ratios and EV multiples). While markets, composed of portfolios of companies, are less susceptible to aging, you could argue that aging equity markets (the US, Japan and Europe) will exhibit different characteristics than they did when were younger and more vibrant.
The second is technology and industry structure, shaking up both the product market structure and creating challenges for accountants. This is true clearly at the company level, as is the case with retailing, where Amazon's entry and subsequent growth has laid waste to historic norms for this sector, bringing down operating margins and changing reinvestment patterns. It is also true at the market level, where an increasing proportion of the equity market (say, the S&P 500) are service and technology stocks and the accounting for expenses in these sectors (with many capital expenses being treated as operating expenses) creating questions about whether the E in the PE for the S&P 500 is even comparable over time.
The third is changes in consumer and investor preferences, with the first affecting the numbers in product markets and the latter in financial markets. For instance, there is an argument to be made that the surge in index funds has altered how stocks are priced today, as opposed to two or three decades ago.
In the context of CAPE, again, and using Shiller's entire database, which goes back to 1871, let's take a quick look at how much both the US economy has grown and changed since 1871 and how those changes have affected the composition of US stocks.

In 1871, coming out of the civil war, the US was more emerging than developed market, with the growth and risk that goes with that characterization. In 1900, the US equity market had become the largest in the world, but 63% of its value came from railroad stocks, reflecting both their importance to the US economy then and their need for equity capital. For most of the next few decades, the US continued on its path as a growth market and economy, though the growth trend was brought to a stop by the great depression. The Second World War firmly established the US as the center of the global economy and the period between 1945 and 2000 represents the golden age of mean reversion, a period where at least in the US, mean reversion worked like a charm not just across stocks but across time. It is worth noting that many of the now-accepted standard practices in both corporate finance and valuation, from using historical risk premiums for stocks to attaching premiums for expected returns to small-cap stocks to believing that value stocks beat growth stocks (with low PBV or low PE as a proxy for value) came from researchers poring over this abnormally mean-reverting financial history. I trace my awakening to the dangers of mean reversion to the 2008 crisis but I believe that the signs of structural change were around me for at least a decade prior. After all, the shift from a US-centric global economy to one that was more broadly based started occurring in the 1970s and continued, with fits and bounds, in the decades after. Similarly, the US dollar's reign as the global currency was challenged by the introduction of the Euro in 1999 and put under further strain by the growth in emerging market currencies.
So, how did 2008 change my thinking about markets, investing and valuation? First, globalization is here to stay and while it has brought pluses, it has already brought some minuses. As I noted in my post on country risk, no investor or company can afford to stay localized any more, since not only do market crisis in one country quickly become global epidemics, but a company that depends on just its domestic market for operations (revenues and production) is now more the exception than the rule. Second, the fact that financial service firms were at the center of the crisis, has had long term consequences. Not only has it led to a loss of faith in banks as well-regulated entities, run by sensible (and risk averse) people, but it has increased the role of central bankers in economies, with perverse consequences. In their zeal to be saviors of the economy, central bankers (in my view) have contributed to an environment of low economic growth and higher risk premiums. Third, the low economic growth and low inflation has resulted in interest rates lower than they have been historically in most currencies and negative interest rates in some. I know that there are many who believe that I am over reacting and that it only a question of time before we revert back to more normal interest rates, higher economic growth and typical inflation but I am not convinced.
From Statistical Significance to Investment Return Payoff
The standard approach to showing mean reversion is start with historical data and establish mean reversion with statistics. I will start with that basis, again using CAPE as my illustrative example, but will then build on it to show why, even if you believe in mean reversion and you base it on sound statistics, it is so difficult to convert statistical significance into market-beating returns.
The statistics
If you were looking at a data series, how would you go about showing mean reversion? There are three simple statistical devices that you can draw. The first is graphical, a scatter plot of the data that shows the mean reversion over time. In the context of CAPE, for instance, this is the graph that you saw in my last post:

Historical data on Shiller CAPEThe problem with this plot is that it is weak evidence for investing, since you don't make money from buying or selling PE but from buying and selling stocks. In fact, even in this plot, you can see that the CAPE case that stocks are over priced is weakened because I have used a 25-year median for comparison. A stronger graphical backing for mean reversion would then graph stock returns in subsequent time periods as a function of the CAPE today, with a higher CAPE (relative to history) translating into lower returns in a future period.

Looking at this data, at least, the evidence seems strong that a high CAPE today goes with lower stock returns in future periods, with the mean reversion becoming stronger for longer time periods.
The relationship between the market timing metric and returns can be quantified in one of two ways. You could compute the correlation between the metric and returns, with a more negative correlation indicating stronger mean reversion. Updating my CAPE/ returns correlation metric, with 10-year returns added to the mix, you can see again the basis for the market timing argument:

You an build on these correlations and run regressions (linear or otherwise) where you regress returns in future periods against the value of the metric today. The results of those regressions, with CAPE as the market metric, are summarized below:

What does this mean? If you buy into mean reversion and can live with the noise or error in your estimate (captured in the R-squared), these regressions back up the correlation findings, insofar as your CAPE-based predictions get more precise for longer time period returns. In fact, if you are one of those who lives and dies by statistics, using today's CAPE of 27.27 in this regression will yield a predicted annualized return of 4.30% on stocks for the next 10 years:
Expected annualized return in next 10 years = 16.24% - 0.0044 (27.27) = 4.30%Scary, right? But before you over react, first recognize that this prediction comes with a standard error and range and second, please read on.
The Investment Action
If you have sat through a statistics class, you have probably heard the oft-repeated caution that "correlation is not causation", a good warning if you are a researcher trying to explain a phenomenon but not particularly relevant, if you are an investor. After all, if you can consistently make a lot of money from a strategy, do you really need to know why? The biggest challenge in investing is whether you can convert statistical significance ( a high correlation or a regression with impressive predictive power) into investment strategy. It is at this level that market timing metrics run into trouble, and using CAPE again, here are the two ways in which you can use the results from the data to change the way you invest.
If you are willing to buy into the notion that the structural changes in the economy and markets have not changed the historical mean reversion tendencies in the CAPE, the most benign and defensible use of the data is to reset expectations. In other words, if you are an investor in stocks today, you should expect to make lower returns for the next 10 years than you have historically. This has consequences for how much investors should save for future retirement or how much states should set aside to cover future contractual obligations, with both set asides increasing because your expected returns are lower.
It is when you decide to use the CAPE findings to do market timing that the tests become more arduous and difficult to meet. To understand what this means, let's go back to the basic asset allocation decision that all investment begins with. Given your risk aversion (a function of both your psychological make-up and the environment you are in) and liquidity needs (a function of your age, wealth and dependents), there is a certain mix of stocks, bonds and cash that is right for you. With market timing, you will alter this mix to reflect your views on desirable (or under priced) markets and undesirable ones. Thus, your natural mix is 60% stocks, 30% bonds and 10% cash, and you believe (using whatever market timing metric you choose) that stocks are over priced, you would lower your allocation to stocks and increase your allocation to either bonds or cash. You could further refine this market timing algorithm for domestic stocks versus foreign stocks or bring in other asset classes such as collectibles and real estate. The test of a market timing strategy therefore requires more structure than the statistical analysis of checking for correlation or regression:
Timing threshold: If you decide that you will time markets using a metric, you have to follow through with specifics. For instance, with CAPE as your market metric, and a high (low) CAPE being used as an indicator of an over valued (under valued) market, you have to indicate the trigger that will initiate action. In other words, does the CAPE have to be 10% higher, 25% higher or 50% higher than the historic average for you to start moving money out of stocks?
Asset class alternatives: If you decide to move money out of stocks, you have to also specify where the money will go and you have four choices.
Holding period: You will have to specify how long you plan to stay with the "market timed" allocation mix, with the answers ranging from a pre-specified time horizon (1 year, 2 years or 5 years) to until the market timing metric returns to safe territory.
Allocation Constraints (if any): The allocation that you have for an asset class can be floored at zero, if you are a long only investor, but can be negative, if you are willing to go short. The cap on what you can allocate to an asset class is 100%, if you cannot or choose not to borrow money, but can be greater than 100%, if you can.
Put simply, the lower your threshold, the more alternatives you have to investing in stocks, the shorter your holding period and the fewer your constraints, the more active you are as a market timer. It is in this context that I tried out different market timing strategies built around CAPE. The table below lists out the returns from a buy and hold strategy with a fixed mix of stocks, bonds and bills (60%, 30% and 10%) and contrasts it with returns over the same period from using a CAPE timing strategy of reducing the equity allocation to 40% if the CAPE is 25% higher than a 50-year median value and increasing the equity allocation to 80% if the CAPE is 25% lower than a 50-year median value. I report the numbers for the entire time period 1917-2016 and break it down into two fifty-year time periods (1917-1966, 1967-2016):
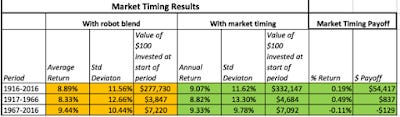
Download market timing spreadsheetWith this mix of timing choices (50-year median, 25% threshold and the given changes to equity allocation), the Shiller CAPE outperforms the buy and hold strategy for the 1917-2016 time period but under performs in the last fifty year time period. I know that your timing choices can be very different from mine and I have created options in this spreadsheet to let you change the choices to reflect your preferences to see if you can deliver better market timing results using CAPE. I did try a few variants and here is what I found.
Time Period: With every variation of timing that I tried, the CAPE delivers a positive market timing payoff in the first half of the entire time period (from 1917 to 1966) and a negative one in the second half (1967-2016). In fact, I could not find a combination of timing devices that delivered positive payoff in the second time period.
Choice of median: Using the lifetime median delivers better results during the "good" period (1917-1966) but worse results during the "bad" period (1967-2016). Using a shorter time periods for the median reduces the outperformance in the first half of the analysis period but improves it in the second half.
Buy and Sell: The CAPE's timing payoff is greater when it is used as a buying metric than as a selling metric. In fact, you make a positive payoff from using a low CAPE as a buying indicator over the entire period but using it is a signal of over priced markets costs you money in both time period.
Market Timing magnitude: Increasing the degree to which you tilt towards or away from stocks, in reaction to the CAPE, just magnifies the return difference, positive or negative. Thus, in the first half of the century (1917-1966), changing your equity exposure more increases the payoff to market timing. In the second half, it makes the negative payoff worse.
In many ways, this testing is tilted in favor of finding that the Shiller CAPE works. First, while I have been careful not to use ex-post data, I have acted as if I know what the earnings for the year will be, at the end of each year, when my market timing decision is made. In reality, on December 31, 2012, I would know only the earnings for the first three quarters of 2012 and not quite the full year. Second, I am ignoring the transactions costs and taxes due from shifting large amounts in and out of stocks in my timing years. Those will represent a significant drain on my returns as an investor. Finally, I am assuming that there have been no structural shifts large enough to cause the mean reversion to break down. In spite of all of this, I am hard pressed to explain why we are so swayed by arguments based on this metric.
Conclusion
These are dangerous times for those who believe in mean reversion, for two reasons. The first is that our access to historical data is getting broader and deeper, with mixed consequences. Having more data allows us to find out more about the underlying fundamentals but since that data goes back so far, much of what we find no longer has relevance. The second is that doing statistical analysis no longer requires either homework or effort, with tools at our fingertips and statistical results are only a click away. Both in academia and in practice, I see more and more use of statistical significance as proof that you can beat markets and my reason devising and testing out market timing strategies with CAPE were not meant to be an assault on CAPE but more a cautionary note that statistical correlation is not cash in the bank. This may also explain why there are so many ways to beat the market, on paper, and so few seem to be able to deliver those magical excess returns, in practice.
YouTube Video
Datasets